Outils de dérivation vectorielle

Genre:

Rating

Outils de dérivation vectorielle Cinématique du solide SMP 3

Sommaire

Dérivation directe ou en coordonnées cartésiennes

Soit un vecteur $\displaystyle\black{\vec{{V}}}$ repéré dans le repère $\displaystyle\black{R}{\left({O},{\vec{{x}}},{\vec{{y}}},{\vec{{z}}}\right)}$ par $\displaystyle\black{\vec{{V}}}={x}.{\vec{{x}}}+{y}.{\vec{{y}}}+{z}.{\vec{{z}}}$ . La dérivée temporelle de ce vecteur par rapport au repère R s'écrit :

$\displaystyle\black{\left[\frac{{{d}{\vec{{V}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}=\frac{{{\left.{d}{x}\right.}}}{{{\left.{d}{t}\right.}}}.{\vec{{x}}}+{x}.{\left[\frac{{{d}{\vec{{x}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}+\frac{{{\left.{d}{y}\right.}}}{{{\left.{d}{t}\right.}}}.{\vec{{y}}}+{y}.{\left[\frac{{{d}{\vec{{y}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}+\frac{{{\left.{d}{z}\right.}}}{{{\left.{d}{t}\right.}}}.{\vec{{z}}}+{z}.{\left[\frac{{{d}{\vec{{z}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}$

Les vecteurs $\displaystyle\black{\vec{{x}}},{\vec{{y}}}$ et $\displaystyle\black{\vec{{z}}}$ étant constant au cours du temps dans le repère R, leurs dérivées sont nulles, donc :

Pour simplifier l'écriture, on note $\displaystyle\black\frac{{{d}{u}}}{{{\left.{d}{t}\right.}}}={\dot{{u}}}$ donc :

$\displaystyle\black{\left[\frac{{{d}{\vec{{V}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}={\dot{{x}}}.{\vec{{x}}}+{\dot{{y}}}.{\vec{{y}}}+{\dot{{z}}}.{\vec{{z}}}$

Si le vecteur $\displaystyle\black{\vec{{V}}}$ n'est par projeté dans R mais dans un autre repère $\displaystyle\black{R}_{{1}}{\left({O},{\vec{{x}}}_{{1}},{\vec{{y}}}_{{1}},{\vec{{z}}}_{{1}}\right)}$ en mouvement par rapport à R, son expression devient alors $\displaystyle\black{\vec{{V}}}={x}.{\vec{{x}}}_{{1}}+{y}.{\vec{{y}}}_{{1}}+{z}.{\vec{{z}}}_{{1}}$ . Les vecteurs $\displaystyle\black{\vec{{x}}}_{{1}},{\vec{{y}}}_{{1}}$ et $\displaystyle\black{\vec{{z}}}_{{1}}$ n'étant pas forcement constants au cours du temps dans le repère R, leurs dérivées sont non nulles.

Donc il faut:

soit projeter le vecteur $\displaystyle\black{\vec{{V}}}$ dans R. Les calculs deviennent alors assez lourds du fait de l'apparition de fonctions sin et cos à dériver.
soit de calculer $\displaystyle\black{\left[\frac{{{d}{\vec{{x}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}},{\left[\frac{{{d}{\vec{{y}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}$ et $\displaystyle\black{\left[\frac{{{d}{\vec{{z}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}$ (voir paragraphe suivant)

Dérivation composée - Formule de Bour

Dérivée temporelle d'un vecteur unitaire par rapport à un repère- Cas particulier d'une seule rotation

Soit $\displaystyle\black{\left({\vec{{x}}}_{{1}},{\vec{{y}}}_{{1}},{\vec{{z}}}_{{1}}\right)}$ la base d'un repère $\displaystyle\black{R}_{{1}}$ mobile par rapport à R.

Dans un premier temps, on considère que $\displaystyle\black{R}_{{1}}$ est orienté par une seule rotation autour d'un axe de R, par exemple une rotation d'angle $\displaystyle\black\psi$ autour de $\displaystyle\black{\vec{{z}}}$ alors : $\displaystyle\black{\vec{{x}}}_{{1}}={\cos{\psi}}{\vec{{x}}}+{\sin{\psi}}{\vec{{y}}}$ et $\displaystyle\black{\vec{{y}}}_{{1}}={\cos{\psi}}{\vec{{y}}}-{\sin{\psi}}{\vec{{x}}}$

$\displaystyle\black{\left[\frac{{{d}{\vec{{x}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}=-{\dot{\psi}}{\sin{\psi}}{\vec{{x}}}+{\dot{\psi}}{\cos{\psi}}{\vec{{y}}}={\dot{\psi}}{\vec{{y}}}_{{1}}={\dot{\psi}}{\vec{{z}}}\wedge{\vec{{x}}}_{{1}}$ et

$\displaystyle\black{\left[\frac{{{d}{\vec{{y}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}=-{\dot{\psi}}{\cos{\psi}}{\vec{{x}}}+{\dot{\psi}}{\sin{\psi}}{\vec{{y}}}=-{\dot{\psi}}{\vec{{y}}}_{{1}}={\dot{\psi}}{\vec{{z}}}\wedge{\vec{{y}}}_{{1}}$

et comme $\displaystyle\black{\vec{\Omega}}_{{{R}_{{1}}\//{R}}}={\dot{\psi}}{\vec{{z}}}$ on a :

$\displaystyle\black{\left[\frac{{{d}{\vec{{x}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}={\vec{\Omega}}_{{{R}_{{1}}\//{R}}}\wedge{\vec{{x}}}_{{1}}$

$\displaystyle\black{\left[\frac{{{d}{\vec{{y}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}={\vec{\Omega}}_{{{R}_{{1}}\//{R}}}\wedge{\vec{{y}}}_{{1}}$

Généralisation - composition des vitesses de rotation

Soient n bases $\displaystyle\black{R}_{{i}}$ définies les unes par rapport aux autres par des vecteurs vitesse de rotation successifs $\displaystyle\black{\vec{\Omega}}_{{{R}_{{i}}\//{R}_{{{i}-{1}}}}}$ .

On peut écrire : $\displaystyle\black{\vec{\Omega}}_{{{R}_{{n}}\//{R}_{{1}}}}={\vec{\Omega}}_{{{R}_{{n}}\//{R}_{{{n}-{1}}}}}+{\vec{\Omega}}_{{{R}_{{{n}-{1}}}\//{R}_{{{n}-{2}}}}}+\ldots+{\vec{\Omega}}_{{{R}_{{2}}\//{R}_{{1}}}}$

On peut donc généraliser les résultats du paragraphe précédent à un repère $\displaystyle\black{R}_{{1}}$ issu de R par un vecteur vitesse de rotation quelconque $\displaystyle\black{\vec{\Omega}}_{{{R}_{{1}}\//{R}}}$ (et non plus seulement confondu avec un axe de R). On obtient alors :

$\displaystyle\black{\left[\frac{{{d}{\vec{{x}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}={\vec{\Omega}}_{{{R}_{{1}}\//{R}}}\wedge{\vec{{x}}}_{{1}}$

$\displaystyle\black{\left[\frac{{{d}{\vec{{y}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}={\vec{\Omega}}_{{{R}_{{1}}\//{R}}}\wedge{\vec{{y}}}_{{1}}$

$\displaystyle\black{\left[\frac{{{d}{\vec{{z}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}={\vec{\Omega}}_{{{R}_{{1}}\//{R}}}\wedge{\vec{{z}}}_{{1}}$

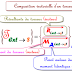
Dérivée temporelle d'un vecteur quelconque par rapport à un repère

Le repère $\displaystyle\black{R}_{{1}}$ est défini par rapport au repère R par son vecteur vitesse de rotation $\displaystyle\black{\vec{\Omega}}_{{{R}_{{1}}\//{R}}}$ quelconque.Soit un vecteur $\displaystyle\black{\vec{{V}}}$ repéré dans le repère $\displaystyle\black{R}_{{1}}{\left({O},{\vec{{x}}}_{{1}},{\vec{{y}}}_{{1}},{\vec{{z}}}_{{1}}\right)}$ par $\displaystyle\black{\vec{{V}}}={x}.{\vec{{x}}}_{{1}}+{y}.{\vec{{y}}}_{{1}}+{z}.{\vec{{z}}}_{{1}}$ .

La dérivée temporelle de $\displaystyle\black{\vec{{V}}}$ dans $\displaystyle\black{R}_{{1}}$ s'écrit :

$\displaystyle\black{\left[\frac{{{d}{\vec{{V}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{{R}_{{1}}}}={\dot{{x}}}.{\vec{{x}}}_{{1}}+{\dot{{y}}}.{\vec{{y}}}_{{1}}+{\dot{{z}}}.{\vec{{z}}}_{{1}}$

Si on cherche sa dérivée temporelle par rapport à R :

$\displaystyle\black{\left[\frac{{{d}{\vec{{V}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}={\dot{{x}}}.{\vec{{x}}}_{{1}}+{\dot{{y}}}.{\vec{{y}}}_{{1}}+{\dot{{z}}}.{\vec{{z}}}_{{1}}+{x}.{\left[\frac{{{d}{\vec{{x}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}+{y}.{\left[\frac{{{d}{\vec{{y}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}+{z}.{\left[\frac{{{d}{\vec{{z}}}_{{1}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}$

$\displaystyle\black{\left[\frac{{{d}{\vec{{V}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}={\dot{{x}}}.{\vec{{x}}}_{{1}}+{\dot{{y}}}.{\vec{{y}}}_{{1}}+{\dot{{z}}}.{\vec{{z}}}_{{1}}+{x}.{\vec{\Omega}}_{{{R}_{{1}}\//{R}}}\wedge{\vec{{x}}}_{{1}}+{y}.{\vec{\Omega}}_{{{R}_{{1}}\//{R}}}\wedge{\vec{{y}}}_{{1}}+{z}.{\vec{\Omega}}_{{{R}_{{1}}\//{R}}}\wedge{\vec{{z}}}_{{1}}$

$\displaystyle\black{\left[\frac{{{d}{\vec{{V}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}={\dot{{x}}}.{\vec{{x}}}_{{1}}+{\dot{{y}}}.{\vec{{y}}}_{{1}}+{\dot{{z}}}.{\vec{{z}}}_{{1}}+{\vec{\Omega}}_{{{R}_{{1}}\//{R}}}\wedge{\left({x}{\vec{{x}}}_{{1}}+{y}.{\vec{{y}}}_{{1}}+{z}.{\vec{{z}}}_{{1}}\right)}$

D'où :


Formule de Bour
$\displaystyle\black{\left[\frac{{{d}{\vec{{V}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{R}}={\left[\frac{{{d}{\vec{{V}}}}}{{{\left.{d}{t}\right.}}}\right]}_{{{R}_{{1}}}}+{\vec{\Omega}}_{{{R}_{{1}}\//{R}}}\wedge{\vec{{V}}}$

Posted on

Popular Posts

Articles les plus consultés

livres scientifiques

About us

Breaking News

Business

Flickr Images